Exercises 15 18 Evaluate the Integral Using the Method Described
Considering xto be constant and integrating with respect to. Tan dÐ In x x-2e-lX dr cot de x Inx.
We can evaluate this new integral by using integration by parts again.
. Next evaluate the same integral using the substitution x csc θ. Evaluate Integrals Involving Quadratic Expressions Using Completing Square Tutorials with examples and detailed solutions and exercises with answers on how to use the techniques of completing square and substitution to evaluate integrals involving quadratic expressions. Fxx3 3x2 2x6 16.
415 parts per million 19. B The region of integration R showing the order dx dy. Exercises 3564 use integration the Direct Comparison Test or Limit Comparison Test to test the integrals for convergence.
Use the Shell Method to find the volume of the solid of revolution formed by rotating the region about each of the given axes. Pi 7j t 1k dt Го- 4 k dt 2. Calculate the integral x x 1dx.
Chapter 62 Problem 18E is solved. Example 2 The Integral of an Integral. Edited May 5 2013 at 900.
Fx1 3 x3 5 2 x2 4x. These integrals are known as line integrals over vector fields. Step 3 of 5.
Evaluate the integral exactly. X sec θ. A R is the triangle with vertices at the origin 02 and.
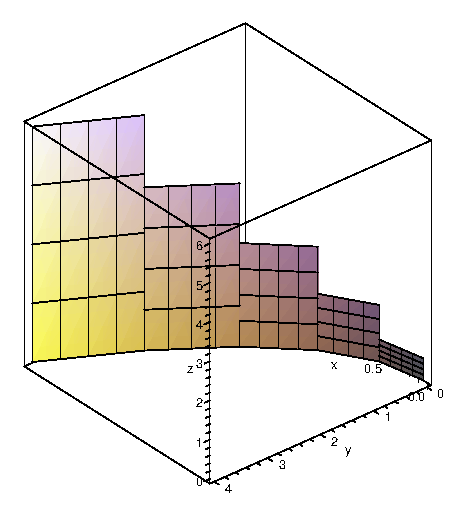
View a sample solution. Just as a vector field is defined by a function that returns a vector a scalar field is a function that returns a scalar such as z f. 152 Double Integrals over General Regions 865 FIGURE 1518 a The solid wedgelike region whose volume is found in Example 4.
Split the integral and try to find out 0 a x 2 a 2 using integration by parts. If than one method applies use whatever method you prefer. Regions are parts of cones cylinders spheres and pyramids 10 m Question.
Show all the workings and explain the methods used. 4Use the residue theorem to compute Z C gzdz. Solution for Evaluate the integrals in Exercises 1K.
Definition 1511 Line Integral Over A Scalar Field. Thus d u d x and v 2 3 e 3 x d x 2 9 e 3 x. Follow this answer to receive notifications.
To do this choose u x and d v 2 3 e 3 x d x. Fundamental Theorem of Calculus Part 1. In Exercises 1318 write a Riemann sum and then a definite integral representing the volume of the region using the slice shown.
6 6ti 3Vij T4 sin ti 1 cos tj sec²tk dt. Its meaning is discussed in the paragraph preceding Definition 1531 when it is compared to a vector field. 5Combine the previous steps to deduce the value of the integral we want.
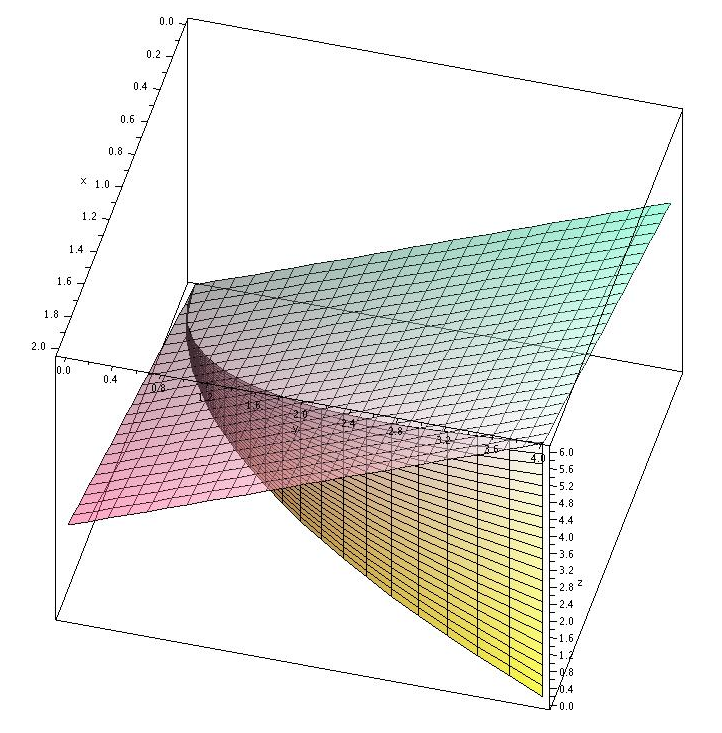
100 3 ratings for this solution. S x y z R3. 16 1 2 y x z y 5 4x 2 2 z 5 216 x2 2 y2 y 5 2x a b 0 05 1 2 1 2 x y y 2 5 4x 2 y 5 2x R x 5 4 y2 x 5 4 y1 2 Exercises 152 Sketching Regions of.
The above leads to du dx. Xx 1dx u 1 u1 2 dx. Use the solving method described in.
Assuming that a 2 x 2 for real a x note that 0 a d x x x 2 a 2 1 a 2 0 a x x 2 a 2 d x. Use the method described in Notes I to supply the limits of integration. B Evaluate the integral using the shadow method.
U x d v 2 3 e 3 x d x d u d x v 2 3 e 3 x d x 2 9 e 3 x. Otherwise the improper integral diverges. Example 1 Integrating with Respect to y.
I s 2x dxdydz where the solid S is defined as. We must evaluate two integrals as we have two different sample slices. As mentioned earlier the Fundamental Theorem of Calculus is an extremely powerful theorem that establishes the relationship between differentiation and integration and gives us a way to evaluate definite integrals without using Riemann sums or calculating areas.
An improper integral is defined in terms of a limit. 2Pick a closed contour Cthat includes the part of the real axis in the integral. Step 1 of 5.
View this answer View this answer View this answer done loading. A line integral is an integral of the form. It should be such that we can computeZ gzdzover each of the pieces except the part on the real axis.
X 0. Where possible with the techniques from the class evaluate the integral. In the following exercises evaluate the integral using area formulas.
Let u x 1 which gives x u 1. Step 2 of 5. Each slice has area 3 x so the total area using nintervals is given by Total area ˇ Xn i1 3 x i Taking the limit as n1or x0 and noting that the rst slice is at x 0 and the last slice is at x 5 Total area Z x5 x0 3 dx 3x 5 0 35 0 15 sq.
For some of them it may be necessary to break the integral up into two parts. Solution to Example 2. A A 625 b 42 meters c 12037 kilometers per hour.
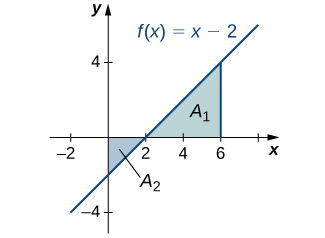
Use the solving method described in. In each case begin by sketching the region. The integral is the area of the triangle 19.
Let C be a smooth curve parameterized by s the arc-length parameter and let f be a continuous function of s. 3The contour will be made up of pieces. The integral in Example 2 is an iterated integral.
An integral over an infinite interval or an integral of a function containing an infinite discontinuity on the interval. The integral is the area of the triangle 9. The volume can be computed as.
X2 y2 4z2 1 a Describe or sketch the solid S. Use Integration by Substitution. In the following exercises evaluate the integrals of the functions graphed using the formulas for areas of triangles and circles and subtracting the areas below the latexxlatex-axis.
This is a way to check the answer to integrals calculations. The improper integral converges if this limit is a finite real number. In exercises 128 evaluate the integrals.
By contrast the line integrals we dealt with in Section 151 are sometimes referred to as line integrals over scalar fields. Using the result of Example 1 you have. The objective is to evaluate the integral.
0 y 2z 1. Evaluate the integral d x x x 2 1 d x x x 2 1 using the substitution x sec θ. In Exercises 13 18 a region of the Cartesian plane is described.
5 2 The Definite Integral Calculus Volume 1
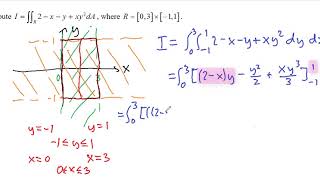
Double Integrals Volume And Average Value
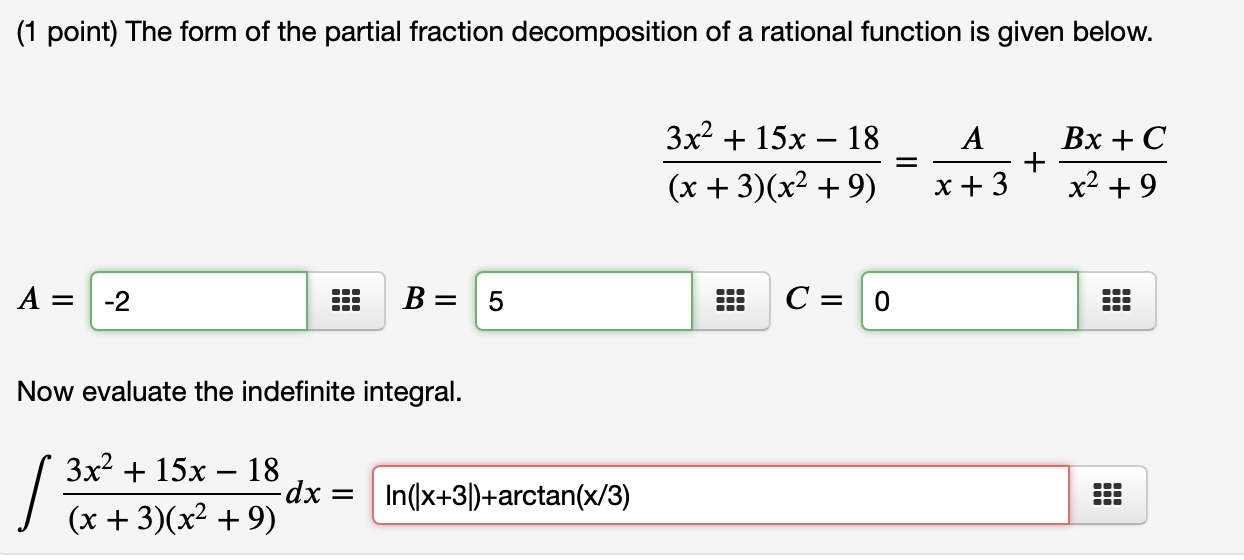
Solved 1 Point The Form Of The Partial Fraction Chegg Com
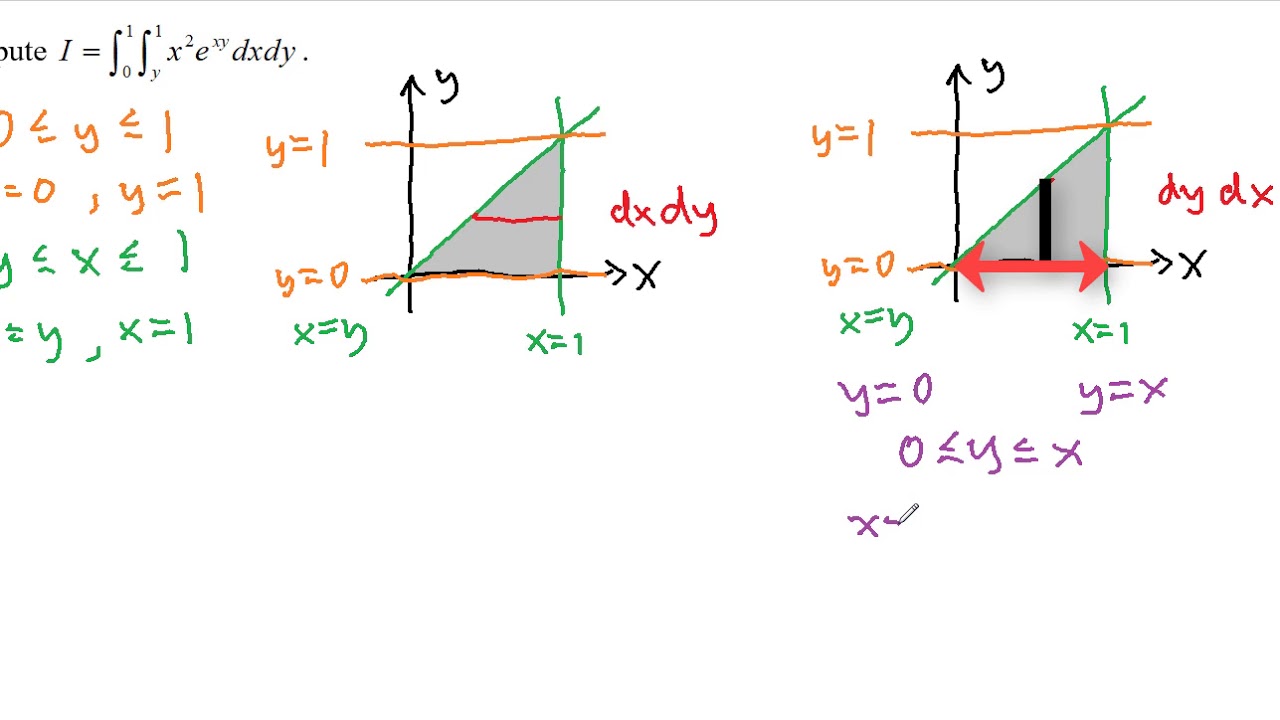
Double Integrals Volume And Average Value
5 2 The Definite Integral Calculus Volume 1

5 2 The Definite Integral Calculus Volume 1
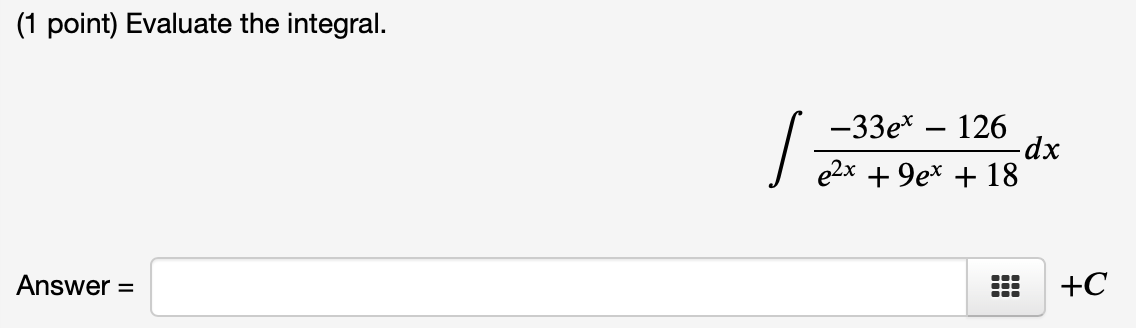
Solved 1 Point The Form Of The Partial Fraction Chegg Com
Calculus Lesson 15 Relation Between Differentiation And Integration Don T Memorise Youtube

Average Value And Area Revisited
Double Integrals Over General Regions Calculus Volume 3
Double Integrals Over General Regions Calculus Volume 3
5 2 The Definite Integral Calculus Volume 1

Quantifying Cell Cycle Dependent Drug Sensitivities In Cancer Using A High Throughput Synchronisation And Screening Approach Ebiomedicine

Finding Derivative With Fundamental Theorem Of Calculus Video Khan Academy
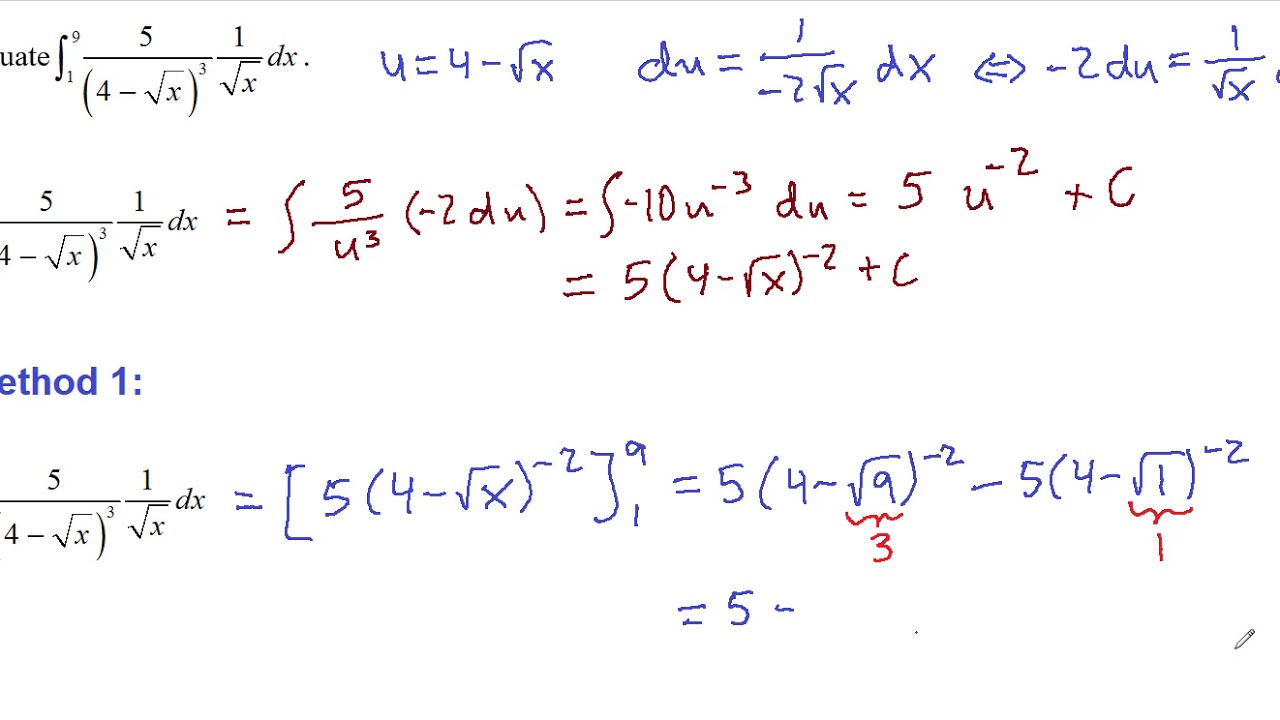
Comments
Post a Comment